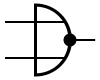
COMPUERTA LÓGICA NOR
La compuerta NOR es una cámara digital puerta lógica que implementa lógica NOR - se comporta de acuerdo a la tabla de verdad a la derecha. Una salida de alta (1) si los resultados tanto de las entradas a la puerta son LOW (0).Si uno o ambos de entrada es HIGH (1), una salida bajo (0) resultados. NI es el resultado de la negación de la Operador. Tampoco es un completamente funcional operación de combinaciones de puertas NO se pueden combinar para generar cualquier función lógica otros. Por el contrario, el O operador es monótono, ya que sólo se puede cambiar a LOW viceversa alto, pero no.
En la mayoría, pero no todas, las implementaciones de circuitos, la negación viene de forma gratuita, incluyendoCMOS y TTL . En las familias en esa lógica, la única manera de poner en práctica o es con dos o más puertas, como un NOR seguida de un inversor. Una excepción importante es que algunas formas de la lógica del dominó de la familia.
El original equipo de Apolo Orientación utilizado 4.100 circuitos integrados, cada uno con un solo 3-input NI puerta
En la mayoría, pero no todas, las implementaciones de circuitos, la negación viene de forma gratuita, incluyendoCMOS y TTL . En las familias en esa lógica, la única manera de poner en práctica o es con dos o más puertas, como un NOR seguida de un inversor. Una excepción importante es que algunas formas de la lógica del dominó de la familia.
El original equipo de Apolo Orientación utilizado 4.100 circuitos integrados, cada uno con un solo 3-input NI puerta
TABLA:
ENTRADA SALIDA
A, B A ni B
0 0 1
0 1 0
1 0 0
1 1 0
SÍMBOLOS:
Hay tres símbolos de puertas NOR: la estadounidense (ANSI o "militar") y el símbolo de la IEC ("europeo" o "rectangular") símbolo, así como la obsoleta DIN símbolo. Para más información, consulte Símbolos Compuerta lógica .
Puerta OR-exclusiva (XOR)
Símbolo de la función lógica O-exclusiva: a) Contactos, b) Normalizado y c) No normalizado
La puerta lógica OR-exclusiva, más conocida por su nombre en inglés XOR, realiza la función booleana A'B+AB'. Su símbolo es el más (+) inscrito en un círculo. En la figura de la derecha pueden observarse sus símbolos en electronica.
La ecuación característica que describe el comportamiento de la puerta XOR es:
Su tabla de verdad es la siguiente:
| Entrada A | Entrada B | Salida 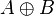 |
|---|---|---|
Se puede definir esta puerta como aquella que da por resultado uno, cuando los valores en las entradas son distintos. ej: 1 y 0, 0 y 1 (en una compuerta de dos entradas). Se obtiene cuando ambas entradas tienen distinto valor.
Si la puerta tuviese tres o más entradas , la XOR tomaría la función de suma de paridad, cuenta el número de unos a la entrada y si son un número impar, pone un 1 a la salida, para que el número de unos pase a ser par. Esto es así porque la operación XOR es asociativa, para tres entradas escribiríamos: a\oplus(b\oplusc) o bien (a\oplusb)\oplusc. Su tabla de verdad sería:
| Entrada A | Entrada B | Entrada C | Salida  |
|---|---|---|---|
Desde el punto de vista de la aritmética módulo 2, la puerta XOR implementa la suma módulo 2.
COMPUERTA LÓGICA NAND
La operación NAND es una operación lógica de dos valores lógicos , por lo general los valores de dos proposiciones , que produce un valor de false si y sólo si ambos operandos son verdaderos. En otras palabras, que produce un valor de verdadero si y sólo si al menos uno de sus operandos es falso.
Tabla de verdad
La tabla de verdad de A y B NAND (también escrito como A | B, DPQ, o A, B ↑) es el siguiente:
Tabla de verdad
La tabla de verdad de A y B NAND (también escrito como A | B, DPQ, o A, B ↑) es el siguiente:
ENTRADA SALIDA A B A, B NAND 0 0 1 0 1 1 1 0 1 1 1 0
PROPIEDADES: NAND no posee ninguna de las cinco propiedades, cada una de las cuales está obligado a estar ausente de, y la ausencia de todo lo cual es suficiente para, al menos un miembro de un conjunto de funcionalidad completa de operadores: la verdad, la preservación, la falsedad, preservación, linealidad , monotonía , la auto-dualidad . (Un operador es la verdad (falsedad) la preservación de su valor si es verdad (falsedad) siempre que todos sus argumentos son la verdad (falsedad).) Por lo tanto {NAND} es un conjunto funcionalmente completo.
Esto también se puede realizar de la siguiente manera: Los tres elementos del conjunto funcionalmente completo {AND, OR, NOT} puede ser construido usando sólo NAND . Así, el conjunto {NAND} debe ser funcionalmente completo también.
SÍMBOLOS:
p n de los números naturales n
(|)
La carrera Sheffer desplazamientos, pero no asociado (por ejemplo, (T | T) | F = T, pero T | (T | F) = F). Por lo tanto, cualquier sistema formal que incluye la carrera Sheffer también debe incluir un medio para indicar la agrupación. Vamos a emplear '(' y ')' en este sentido.
También escribimos p, q, r, ... en lugar de p 0, p 1, p 2.
SINTAXIS:
Regla de construcción I: Para cada número natural n, el símbolo p n es una fórmula bien formada (fbf), llamado de un átomo.
La construcción: Si X e Y son BFF, entonces (X | Y) es una fbf.
Regla de cierre: Cualquier fórmula que no se puede construir a través de las Normas de Construcción de las dos primeras no son BFF.
Las letras U, V, W, X e Y son metavariables pie de BFF.
Un procedimiento de decisión para determinar si una fórmula es bien formada es la siguiente: "deconstruir" la fórmula mediante la aplicación de las normas de construcción al revés, rompiendo así la fórmula en pequeñas subfórmulas. A continuación, repita este proceso de deconstrucción recursiva para cada uno de los subfórmulas. Finalmente, la fórmula debe ser reducido a sus átomos, pero si algún subfórmula no puede ser tan reducido, entonces la fórmula no es una fbf
FAMILIAS DE MICROPROCESADORES CMOS
Complementará metal-oxide-semiconductor o CMOS es una de las familias lógicas empleadas en la fabricación de circuitos integrados. Su principal característica consiste en la utilización conjunta de transistores de tipo pMOS y tipo nMOS configurados de tal forma que, en estado de reposo, el consumo de energía es únicamente el debido a las corrientes parásitas.
En la actualidad, la mayoría de los circuitos integrados que se fabrican utilizan la tecnología CMOS. Esto incluye microprocesadores, memorias, procesadores digitales de señales y muchos otros tipos de circuitos integrados digitales cuyo consumo es considerablemente bajo.
En un circuito CMOS, la función lógica a sintetizar se implementa por duplicado mediante dos circuitos: uno basado exclusivamente en transistores pMOS (circuito de pull-up), y otro basado exclusivamente en transistores nMOS (circuito de pull-Down). El circuito pMOS es empleado para propagar el valor binario 1 (pull-up), y el circuito nMOS para propagar el valor binario 0 (pull-Down). Véase la figura. Representa una puerta lógica NOT o inversor.
Cuando la entrada es 1, el transistor nMOS está en estado de conducción. Al estar su fuente conectada a tierra (0), el valor 0 se propaga al ordenador y por lo tanto a la salida de la puerta lógica. El transistor pMOS, por el contrario, está en estado de no conducción.
Cuando la entrada es 0, el transistor pMOS está en estado de conducción. Al estar su fuente conectada a la alimentación (1), el valor 1 se propaga al ordenador y lo tanto a la salida de la puerta lógica. El transistor nMOS, por el contrario, está en estado de no conducción.
Otra de las características importantes de los circuitos CMOS es que son regenerativos: una señal degradada que acometa una puerta lógica CMOS se verá restaurada a su valor lógico inicial 0 ó 1, siempre y cuando aún esté dentro de los márgenes de ruido que el circuito pueda tolerar.
FAMILIAS DE MICROPROCESADORES TTL
El primer transistor-transistor lógica de la familia de circuitos integrados fue presentado por Sylvania Sylvania universal como de Alto Nivel de la lógica (Suhl) en 1963. Texas Instruments introdujo la serie 5400 de la familia TTL en 1964.
Lógica transistor-transistor utiliza transistores bipolares para formar los circuitos integrados. [3] TTL ha cambiado significativamente en los últimos años, con nuevas versiones de reemplazo de los tipos más antiguos.
Puesto que los transistores de una puerta TTL estándar son interruptores saturadas, los portadores minoritarios en el tiempo de almacenamiento en cada cruce los límites de la velocidad de conmutación del dispositivo. Las variaciones en el diseño básico del TTL tienen la intención de reducir estos efectos y mejorar la velocidad, el consumo de energía, o ambos.
El físico alemán Walter H. Schottky formuló una teoría predecir el efecto Schottky, que llevó a la diodo Schottky y más tarde de transistores Schottky. Transistores Schottky tiene una velocidad de conmutación mucho más altos que los transistores convencionales porque la unión Schottky no promueve el almacenamiento de carga, lo que lleva a las puertas de conmutación rápida. Gates construido con los transistores Schottky utilizan más energía de lo normal TTL y cambiar más rápido. Con Schottky de baja potencia (LS), los valores de resistencia interna se incrementa para reducir el consumo de energía y aumentar la velocidad de conmutación en la versión original. La introducción de avanzada Schottky de baja potencia (ALS) aumentó aún más velocidad y menor consumo de energía. Una familia lógica más rápido llamado Fast (Schottky) (F) se introdujo también que era más rápido que lo normal TTL Schottky.